Hi, everybody. This is Uchida from TVLogic.
On the following pages, I would like to provide some lessons about motion picture production using LOG images.
These are some of the topics:
First of the all, what is a LOG image?
I want to produce motion pictures using LOG images, but do can I do it?
I am producing motion pictures using LOG images, but how can I improve the efficiency and quality of the process?
I hope to answer these questions and solve your problems.
- Lesson 1: Let's take a look at the graph of the gradation characteristics of several cameras.
- Lesson 2: First of all, what is LOG?
- Lesson 3: " Why do LOG image look dull" Part 1
- Lesson 4: " Why do LOG image look dull" Part 2
- Lesson 5: Why does each camera maker have their own LOG?
- Lesson 6: What is the appropriate exposure for recording with LOG?
※The contents of this lesson are subject to change.
Hi everyone. I'm Mitsuhiro Uchida of TVLogic and I'm going to continue our discussion of LOG in this second lecture. When I ask someone 'what do you think about LOG images of film production,' I usually hear the following:
LOG has wide dynamic range, by not over-exposing for highlights nor crushing shadows.
LOG is dull and has a low saturation look. It is not easy to set up for an accurate exposure.
We cannot see a finalized image, so deciding on lighting effects is difficult.
We want to use LOG images, but we have no ideas how to handle the workflow, etc.
In this lesson, I will nail down these questions, 1.
"What is LOG, when it comes to applying to your image?" and 2. Does using LOG bring wider the dynamic range?"

Now, I would like to give some examples to help you understand the "LOG" concept in the film making industry.
Assume there are 1000 lights in the studio. Let's think about how to express the brightness using these 1000 lights in integers from 0 to 100 (101 steps).
It could be simple if we could use from 0 to 1000 integers as the same number of the lights and express the brightness. However, what if we could we express the brightness using about 1/10 as many numbers?
First of all, let's simply assign the integers from 0 to 100 to the range of 0 to 1000 lights.
By the way, when we represent the integers, which are proportional to the number of
lights (= absolute value for brightness), we call it "linear".
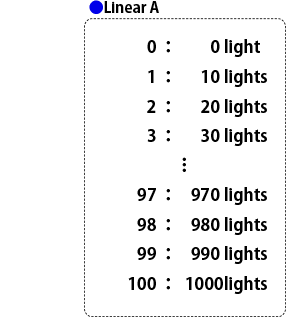
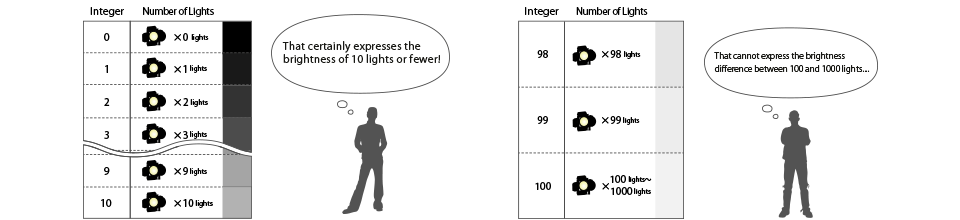
As you have seen in the table, by assigning consecutive integers to every 10 lights, we are able to express 1000 lights brightness with the integers from 0 to 100.
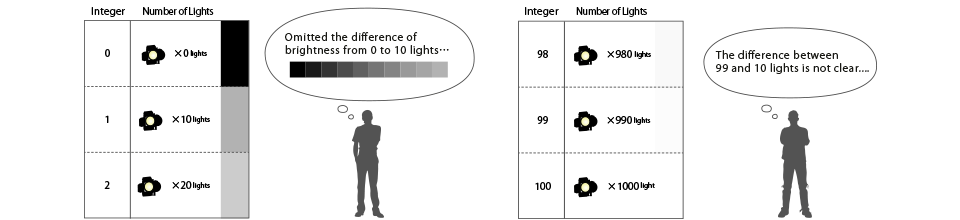
But, in this case, this system omits the difference of brightness from 0 to 10 lights, which our eyes clearly perceive to have a noticeable difference. (There is the same problem expressing the brightness between 10-20 lights.)
Furthermore, this system has another flaw: assigning integers, such as 99 for 990 lights and 100 for 1000 lights, where human beings barely perceive any difference. I would say there seem to be some flaws assigning integers to express higher brightness numbers.
Next, let's assign integers to brightness up to 100 lights to express the brightness difference from 0 to 100 lights.
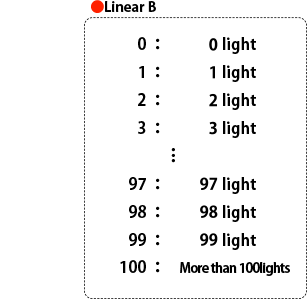
By assigning integers to the number of lights themselves, it enables us to express the brightness difference for less than 10 lights.
In return, it becomes impossible to express the difference for brightness over 100 lights. They are assigned the same integer, 100, to both 101 and 1000 lights.
In this way, you know that if we attempt to express "Linear" in integers,
we end up with having two problems: "a lack of having enough steps in the darker range", and "to avoid the problem,
the linear system has to sacrifice expressing accurate information in the brighter range."
The "LOG" concept appears to solve these two problems described in the previous sub-section.
Consider this simple example:
Assume we turn on one light. Then, if we turn on one more light, it makes double the brightness. However, if we turn on one more, to total 3 lights, we perceive it gets brighter but it is perceived as far less of the difference previously.
It leads to an idea: we cannot perceive the same difference of brightness between one to two and two to three lights.
Then, how many lights do we need to perceive the same change of brightness as one to two lights?
The answer is when four lights are turned on. We perceive it as the same change of brightness as one to two lights. In other words, our senses perceives (no comma) "when the brightness doubles" and we feel the same degree of change.

The numeric representation of LOG (Logarithm) exactly expresses the situation described above: express the"multiplied change" using summation.
If you observe the above example in the numeric, 1 light = 0, 2 lights= 0.3, 4 lights = 0.6 in LOG, you will see that
"0.3 increased from 1 to 2 lights, 0.3 increased from 2 to 4 lights in LOG. This means they have the same increase respectively.
"This is a significant attribute of LOG: if the same amount of numbers changes, the change of the LOG amount is consistent."
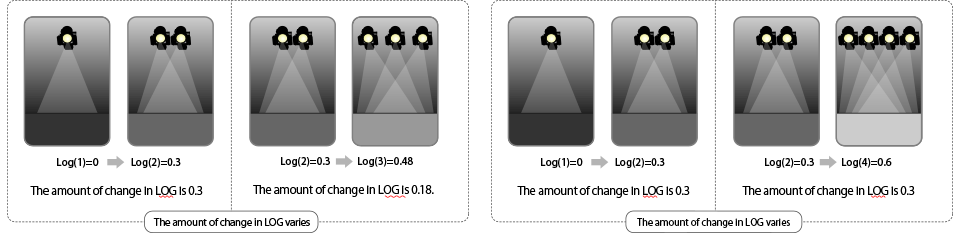

So let's express the brightness of from 0 to 1000 lights in the LOG concept.
Let's use this formula to express the integer change from 0 to 100 as (LOG10 (number of lights) +1)/4*99+1.
It enables us to express the difference from 0 to 10 lights with 51 steps, but also brightness less than 1 is expressed with 25 steps.
On the other hand, this system cannot express the value between 911 lights (expressed 99) and 1000lights (expressed 100). However, if we convert the difference between 991 lights and 1000 lights in a ratio, it is about 1.1 times, which ends up with having the almost same difference in ratio as 0.1 light (expressed 1) and 0.11 light (2). To conclude, the system expresses the same difference that human can perceive.


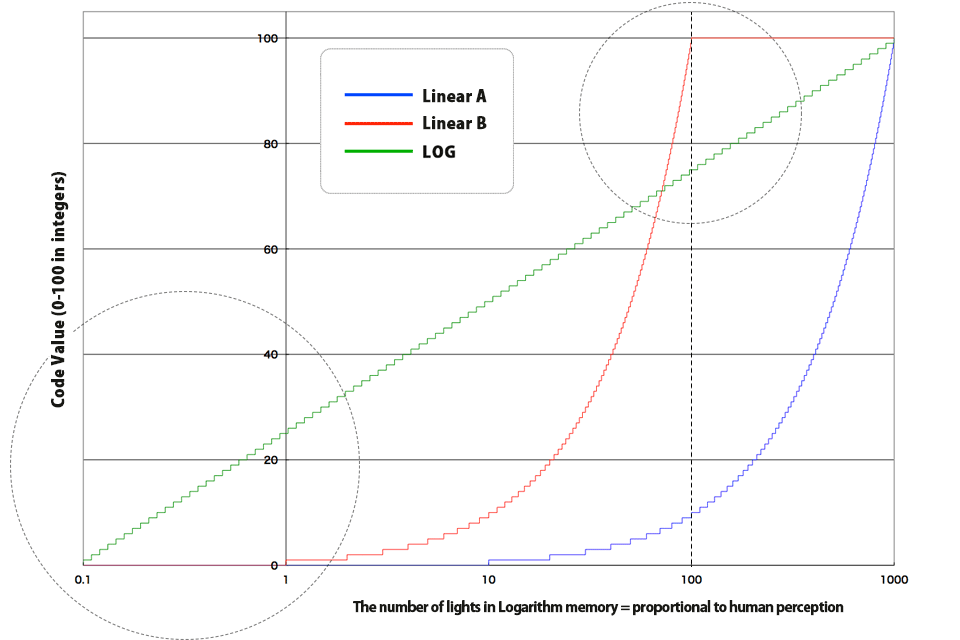
Now, let's examine these explanations so far in a graphical manner.
The horizontal axis represents the number of lights and the vertical axis represents integer from 1 to 100 in the next graph.
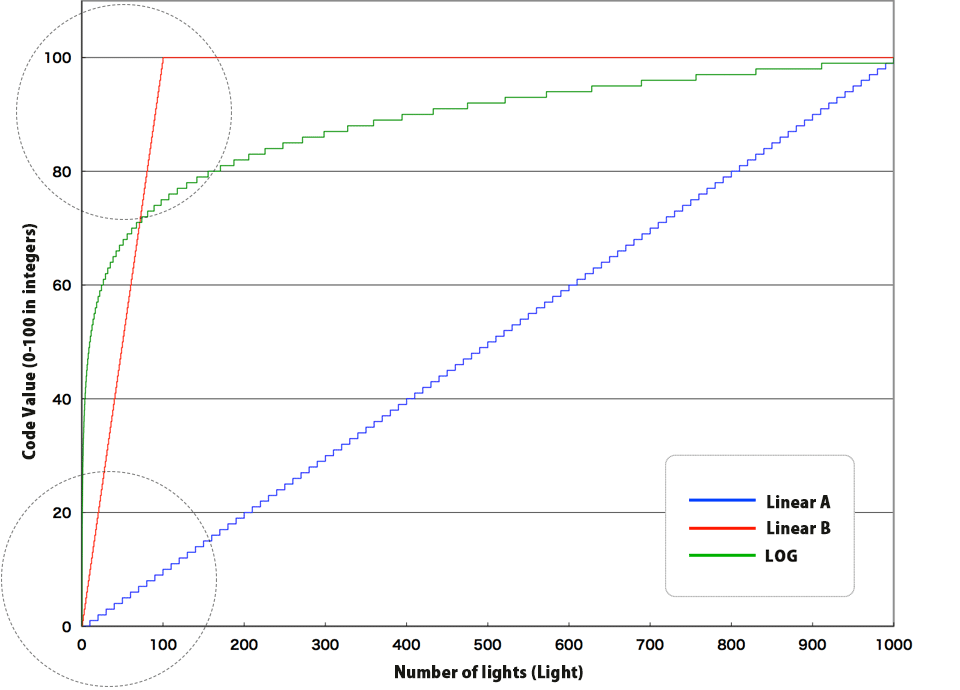
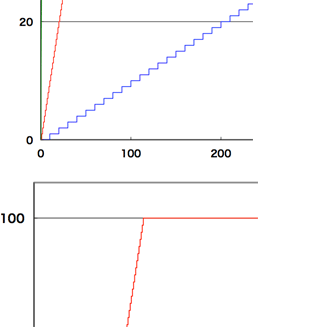
Linear A (blue) expresses the entire range from
0 to 1000 lights, but the lower number values are not expressed precisely.
Linear B (red) has been customized in expressing the lower numbered values, but cannot express the difference between
100 and 1000 lights.
(It is the same as over-exposed and saturated highlights.)
On the other hand, LOG in green seems to express from 0 to 1000, but the line is an obvious curve. Is this acceptable?
Now, let's examine the next graph where the horizontal axis is LOG (=Logarithm) and make sure if this is correct.
The horizontal axis represents the LOG scale, which is close to human perception.
The straight green LOG line it represents is proportional to the human perception.
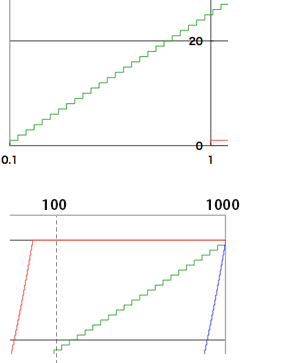
The significant points:
-
This system assigns enough integers to the number of lights that are less than 1 light.
-
At the same time, the system assigns integers to the number of lights that are more than 100.
-
The system assigns the numbers in an equal precise manner from lower to the higher range. Each step in the stair is the same throughout any range in the graph. This means the error diverges evenly into the graph and applies the integer's accuracy effectively.
On the other hand, Linear with a large curve still has critical problems far different from human perception. "Linear A" does not have any assigned number below 10 lights and "Linear B" does not have any assigned number over 100 lights."
There is also problems regarding accuracy where the code values over 60 have smaller errors, which results in seeing no difference in the steps.
On the other hand, the code values under 10 have a different problem where the steps in the stairs are flattened, which makes the amount of change, which is equivalent to 1, of code value larger." To conclude, this lacks accuracy.
As you saw the above, if we use LOG, the system fully maintains the accuracy in the darker area and expresses the brightness in the far higher range at the same time.
This is why "LOG recording is suitable for image types with larger dynamic range."
In this lesson, we used the integers from 0 to 100. If we increase the integer number and use floating-point numbers, i.e. "Linear", which are expressed in the absolute value of brightness, we could express an image with high accuracy. (It is possible to express the proportion without having the steps inline.)
In practical applications like use of regular 10 bits images in film production, only from 0 to 1023 integers will be used. Therefore, this limitation makes LOG beneficial.
In our next lesson, I will continue to explain LOG and examine further: "Why do LOG images look dull?" Please come back for it soon.

Mr. Uchida's profile
He refers to himself as an expert problem solver in image system designs. Starting his career with consumer photos, Mr. Uchida was involved in designing systems using LOG images since 1995 predating the release of Cineon. Currently, he devotes himself enthusiastically to creating solutions which maximize a camera's full feature set with ease.