みなさん、こんにちは。大西です。
映像の色を変えるときに、よく”ラット(LUT)をあてる“と言います。
普段仕事で使うので、なんとなく分かっているようで正しくは分かっていないような”ラット(LUT)“という言葉。
このページでは、今後LUTに関連する解説をします。
みなさまが本ページを読むことで、”なんとなく分かっているもやもや感“が少しでもクリアになると嬉しいです。
- 第一回 LUTの基本
- 第二回 3次元LUTとは?
- 第三回 補間の必要性とLUTの精度について
- 第四回 計算式とLUTの関係
- 第五回 画像の色変換におけるLUTの役割とは?
- 第六回 では実際にLUTはどうやって活用すれば良いの?
※講座の内容は変更になる可能性があります。
第三回 補間の必要性とLUTの精度について
久々の今回は、多くの皆さんが疑問に思うであろう、3DLUTの格子点の数について実験してみようと思います。
8bitの色空間で3DLUTのテーブルを作成することを考えてみます。
8bitの色空間はRGBそれぞれ0-255の256段の整数で表されているので、出現する全種類は、256 x 256 x 256 = 16,777,216 (約1600万)項目の入出力関係をテーブル化しておけばよいことになります。
具体的には、
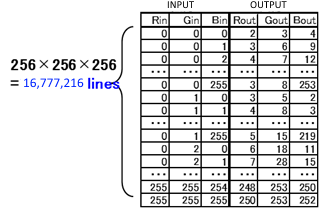
図1
このような感じになります。出力側も8bitとすると、テーブルのサイズは、16,777,216 * 3 = 約50MB と巨大ですが、使用できない大きさではありません。
それでは映像制作で一般的な10bitの色空間ではどうでしょうか。
10bitの色空間は、RGBそれぞれ0-1023の1024段の整数で表されているので、出現する全種類は、1024 x 1024 x 1024 = 1,073,741,824(約10億)項目の入出力関係のテーブルが必要になります。出力側も10bitとすると、テーブルサイズは、 1,073,741,824 * 4 = 4GB と相当巨大なものになります。このサイズのテーブルを高速メモリに搭載して使用したり、動的に生成したり、複数のテーブルを切り替えたりすることは事実上不可能です。
また、浮動小数点の色空間はどうでしょうか。すべての浮動小数点に対応するテーブルを用意することが不可能であることは自明ですね。
そこで登場するのが、「補間」という方法です。
これは、入力色空間の組み合わせすべてに対応するテーブルを用意しておくのでなく、とびとびの、限定された数のテーブルを用意しておき、その間の値については、補間して正しい値を推定する、という方法です。
例えば、下記の表(図2)は8bitの入出力を20ステップずつに間引いたテーブルになっています。
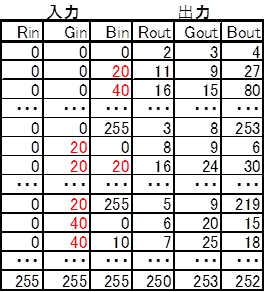
図2
入力(0, 0, 30)に対応する出力は、その前後の(0, 0, 20)と(0, 0, 40)の出力値である(11, 9, 27)と(16, 15, 80)を足して2で割る、などの方法により求めます。
この方法を使えば3DLUTの巨大なテーブルを、かなり小さなテーブルで表すことができるようになります。しかしながら、この「補間」という方法は、どうしても誤差を伴ってしまい、常に正しい値が得られるとは限りません。
ここで簡単な例として、1DLUTの補間を使用して説明します。
図3は8bitの色空間を4つの格子点で表した1DLUTの例です。
黒線のカーブが正しい値であり、
テーブル作成時に●の点を使用しています。
補間して得られる結果が青の折れ線であり、
入力値200の補間結果は●となりますが、
正解値の〇とは大きな誤差が生じていることがわかります。
格子点の数を増やすと、補間誤差は低減されます。
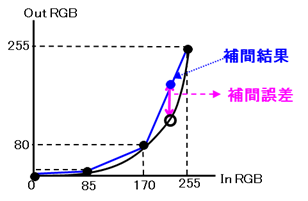
図3
図4の例は、8bitの色空間を7つの格子点で表した例です。図3と比較して、黒の曲線と青の折れ線の差が小さくなっており、補間誤差が軽減していることがわかります。
一方で、補間誤差の現れ方は、変換の種類に大きく依存します。
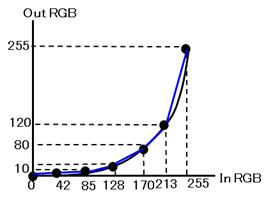
図4
図5は最初の例と同じ、4つの格子点でですが、黒線カーブと青の補間直線との差が小さく、図3に比べて誤差が小さいことがわかります。
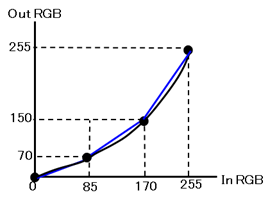
図5
このように、補間には誤差が伴いますが、その大きさはケースバイケースであることがわかります。
3DLUTの場合、格子点の数として、17格子,33格子,65格子などが用いられています。
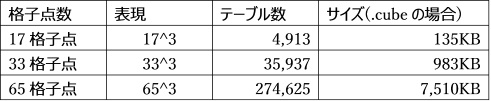
当然のことながら格子点の数が多い方が補間誤差が少なくなり、精度は高くなります。 その代り、ファイルサイズや必要なメモリサイズが大きくなり、読み書きに時間がかかる、システムとして高価になってしまう、などのデメリットがあります。 一般的には、通常は33格子点、システム上可能な場合は65格子点、と使い分けられているようです。
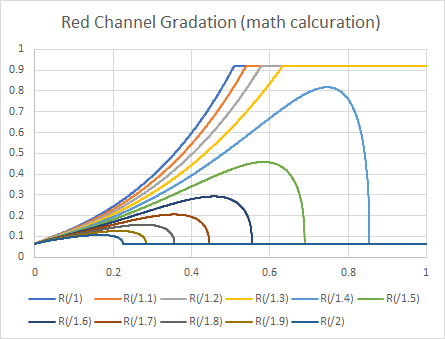
それでは格子点の数で、誤差の表れ方でどのような差がでるのか見てみましょう。
変換は、HDRのRec2020/ST-2084からSDRのRec709/2.4への変換を使用しました。
グラデーションはいろいろ実験した結果、最もバンディングが出やすいシアンのグラデーションを入力素材として使用しました。
画像1が入力画像、グラフ1がそのRチャンネルをグラフ化したものです。
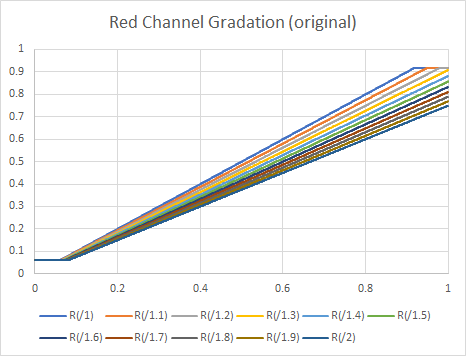
グラフ1
■129格子点
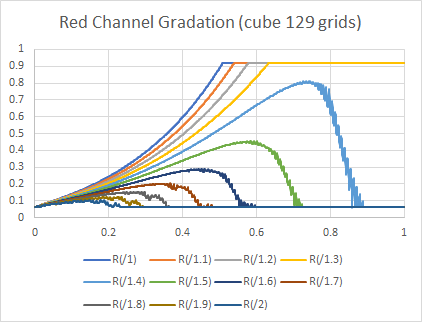
グラフ6
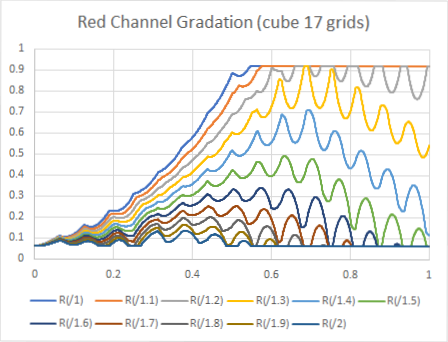
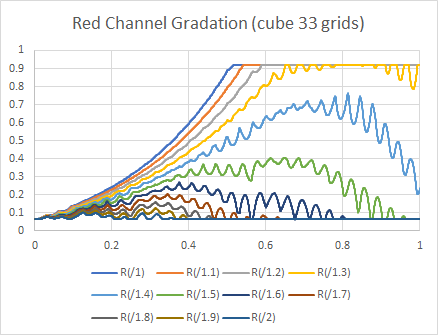
17格子点では、かなり大きな振幅のバンディングが観察され、サンプル画像でもはっきりと確認できます。
格子点の数を増やしていくと、振幅が小さく、周波数が細かくなりますが、129格子点でも取りきることはできません。
計算値と格子点の数を比較するグラフを作ってみました。
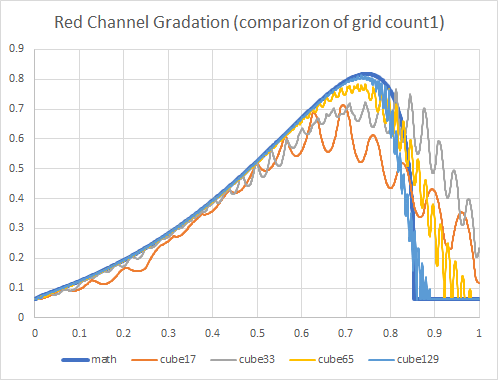
グラフ7
少ない格子点だとバンディングの問題だけでなく、計算値(青線)からの誤差も大きいことがわかります。 格子点の数を増やすと両者とも改善されてきますが、129格子点でも計算値との不一致は残ります。
このようなバンディングや誤差は、補間のアルゴリズムにも依存します。 ここまで紹介してきた結果は、一般的な立方体補間という方法でした。IS-miniでは三角錐補間という、バンディングの出にくいアルゴリズムを採用しており、26格子点というやや少なめの格子点で十分な精度を実現しています。
グラフ8、画像7はIS-miniで処理した結果です。
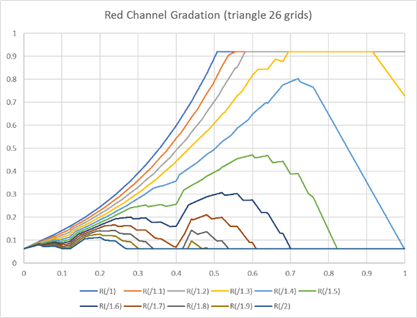
グラフ8
立方体補間の各種格子点の結果と比較してみます。
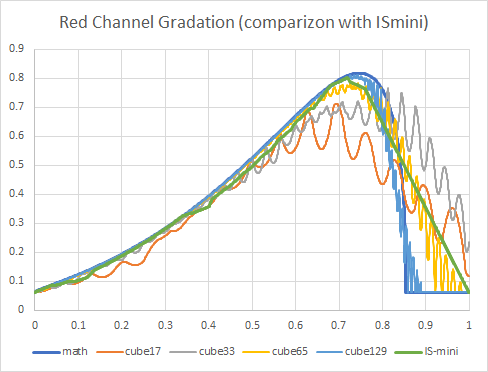
グラフ9
IS-miniの補間誤差は、65格子点とほぼ同等、バンディングはどの格子点数よりも少ない、ことがわかります。
今回の実験結果は、HDR to SDRの変換、シアンのグラデーション、という色再現全体のごく一部の条件における比較ですが、定性的には各種評価結果とほぼ一致した結果となっています。
以上の実験と考察により、
・格子点33が一般的だが、可能であれば65を用いた方が良い
・補間アルゴリズムは立方体補間でなく、三角錐補間の方がバンディングが圧倒的に少なく、誤差も立方体の倍の格子点並みに小さい。
と結論付けられます。