Hi, everybody. I am Onishi of TVLogic.
When we change the color of an image, we usually call it "generating a LUT".
We usually use this term, so we know the meaning of what occurred on-set, but most people don't actually know the meaning of the word "LUT."
On this page, I would like to further explain some information related to LUTs.
I hope this page removes any vagueness you may have on LUTs.
- Lesson 1: Basics about LUT.
- Lesson 2: What is 3D LUT?
- Lesson 3: Necessity for interpolation and accuracy of LUT.
- Lesson 4: Relationship between arithmetic equation and LUT.
- Lesson 5: What is the role of LUT on color conversion on the image.
- Lesson 6: How can we apply LUT in realistically?
※The contents of the lesson are subject to change.
In the first lecture, we explained the basic concept of a 1D LUT. In the last part of the previous lecture, we briefly mentioned that there are some color transformations that a 1D LUT cannot express. Now we are going to explain a 3D LUT using two technical terms, which are "enhancing the tone scale"and" increasing saturation".
I assume you may have heard the following phrase while on-set or a posthouse, "If we enhance the tone scale, saturation will also increase." In fact, this is the typical outcome when we enhance the tone scale using just a 1D LUT.
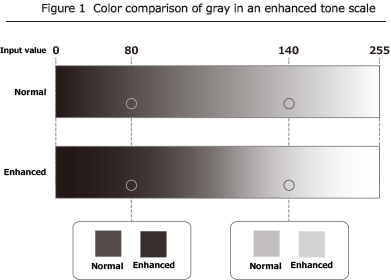
Figure 1 shows the change of the tone scale in an image of gray.
If we enhance the gray tone scale (high contrast), we notice that
"White will be transformed whiter, and black will be darker."
If we reverse the process, we call it "lowering the tone scale (soft tone)".
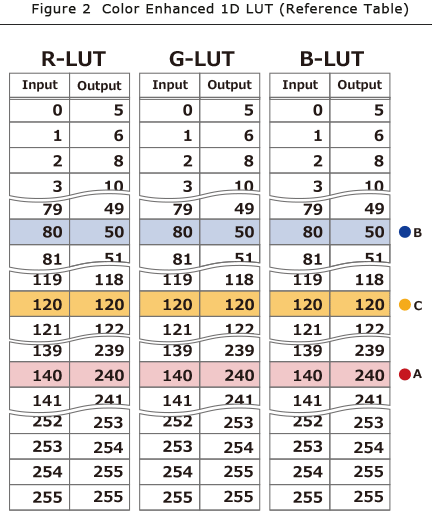
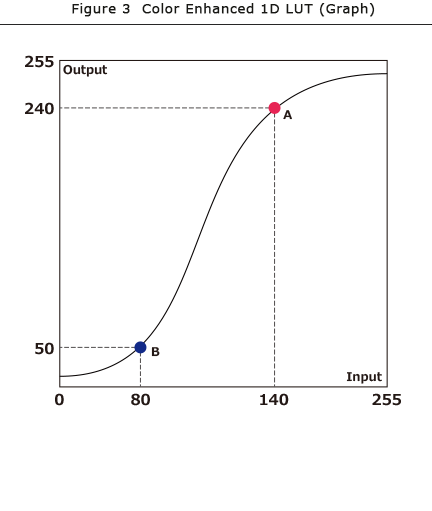
Now, let's take a look at the Figure 2, which shows the numerical result of Figure 1 as an example of 1D LUT and its graph (Figure 3).
In Figure 2, input value of RGB=(140, 140, 140) (●A) will be RGB=(240,240,240) output. In other words, "white will be whiter" in 1D LUT transformation. As the same way we assume the input value of RGB=(80, 80, 80) (●B) will be an output value of RGB= (50,50,50). We definitely know that " black will be darker."
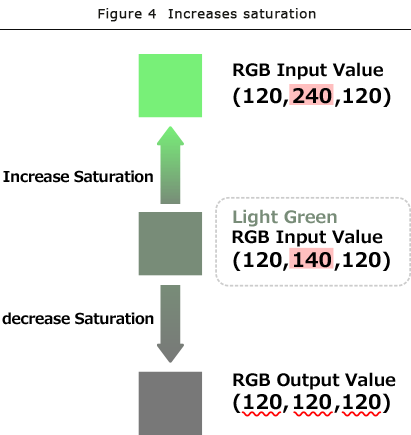
Let's transform light green in Figure 4 which has an input value is RGB= (120, 140, 120) by using a 1D LUT which enables a higher tone scale,.
First, the input value of RGB=(120, 140, 120) will be transformed to output value of RGB=(120, 240, 120).
In this case, we notice "the enhanced element (the value of G) becomes greater than the RGB averaged value." This means saturation is increased numerically."
For your reference, if the tone scale is lowered, conversely, the values of R, G, and B get closer to the RGB average values respectively. The most significant example is when each R, G, and B values are the same as averaged RGB, such as RGB=(120,120 120), the color tone will be achromatic (in this case gray).
Now let's take a look at this case. To enhance the tone scale, we transform gray color at three points; input value of RGB= (80, 80, 80)), RGB= (120, 120, 120), and RGB= (140, 140, 140), to the output value of RGB=(50, 50, 50), RGB=(120, 120, 120), and RGB=(240, 240, 240). A light green input value of RGB=(120, 140, 120) will definitely be transformed to RGB= (120, 240, 120), which results in increased saturation.
Obviously, you can see this numerically; if we attempt to enhance the tone scale by using a 1D LUT, the result will also end up with increased saturation.
Then, what can we do when we want to enhance the gray tone scale but not to increase saturation?
In other words, what could we do when we transform the gray color input value of RGB=(140, 140, 140) to RGB= (2401, 240, 240) output and leave the light green input value of RGB=(120, 140, 120) to RGB=(120, 140, 120) output at the same time?
First, we may just think of rewriting the 1D LUT input value of 140 and output 240 for G to an input of 140 and an output of 140. Then, we would obtain the light green color which has an input value of RGB= (120, 140, 120) and an output value of RGB=(120, 140, 120). However, for a gray tone scale input value of RGB=(140, 140, 140), this would results in a RGB=(240, 140, 240) or an output of magenta color. See Figure 5.
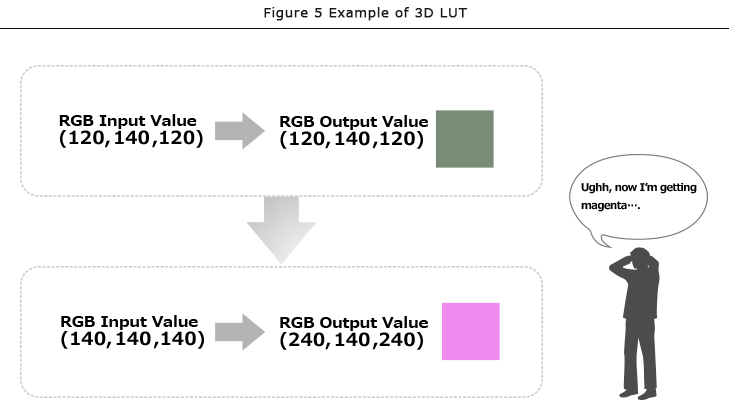
Clearly, it is impossible to satisfy these two transformations with a 1D LUT at the same time. Transforming gray RGB=(140, 140, 140) input values to RGB=(240, 240, 240) output values and light green input of RGB=(120, 140, 120) to RGB=(120, 140, 120) output is just not possible.
So, what can we do then?
There is a simple way to achieve this result. All we have to do is maintain two sets of combinations in the LUT table: input RGB=(140, 140, 140) to output RGB=(240, 240, 240) and input RGB=(120, 140, 120) to output RGB=(120, 140, 120).
In other words, we have to prepare a different type of LUT "A set of the combination of three inputs defining the combination of R, G, and B values; not of one where each input refers to one unique output".
As we see, when we use a LUT that refers to a combination of three values, we call it "3D LUT".
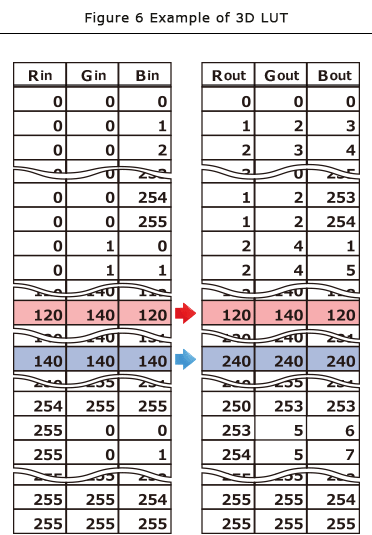
Figure 6 shows examples of an 8bit RGB 3D LUT . The figure shows all combinations of RGB.
If we use a 3D LUT,
input RGB=(120, 140, 120) to output RGB=(120, 140, 120)
input RGB=(140, 140, 140) to output RGB=(240, 240, 240);
These two transformations are possibly executed simultaneously.
If we use a 1D LUT to enhance the gray tone scale of the image in Figure 7, it will increase saturation as we see in Figure 8. However, if we apply 3D LUT to enhance gray tone scale, maintaining saturation simultaneously, we achieve the resulting image found in Figure 9.



By the way, some of you may have noticed that maintaining a 3D LUT as Figure 6 requires a large amount of memory.
In an 8 bit-1D LUT, 256x3=768 combinations of data was only needed. However a 3D LUT needs 256^3=16,777,216 (16.77 millions) combinations.
Therefore, in our next lecture, we will explain about some smart ways on how we can apply a 3D LUT practically while consuming less memory.